CONCEITOS NAO DIFUNDIDOS: Difference between revisions
(Created page with " === 🧩 Núcleo da Teoria da Binarização (Brigitte) === # '''Equivalência Cardinal''' #* Uma combinação proporcional de opções em strikes contíguos pode ser reduzida a uma posição “binária” mais distante. Exemplo: +A30−2A32≡−A34 → Essa equivalência representa '''a compressão de payoff contínuo em uma função binária''' — ou o que Brigitte chama de “cardinalidade equivalente”. #* O raciocínio é que, ao ajustar as proporções (1:-2:...") |
No edit summary |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
Fonte: https://www.youtube.com/watch?v=duSSn5pdCOU | |||
Professor Su | |||
Contribuição chatGPT supervisionado por Mario Caseiro | |||
=== 🧩 Núcleo da Teoria da Binarização (Brigitte) === | === 🧩 Núcleo da Teoria da Binarização (Brigitte) === | ||
| Line 18: | Line 22: | ||
# '''Interpretação Probabilística''' | # '''Interpretação Probabilística''' | ||
#* A operação binarizada pode ser lida como uma '''cadeia de eventos booleanos''' (0 = não exercício, 1 = exercício), ponderada por seus prêmios. | #* A operação binarizada pode ser lida como uma '''cadeia de eventos booleanos''' (0 = não exercício, 1 = exercício), ponderada por seus prêmios. | ||
#* Isso cria um modelo discreto de payoff que se aproxima da curva gaussiana contínua quando replicado em múltiplas escalas (como o princípio de superposição de opções). | #* Isso cria um modelo discreto de payoff que se aproxima da curva gaussiana contínua quando replicado em múltiplas escalas (como o princípio de superposição de opções) | ||
----Mais sobre DUAL e Assunção. TODO: este artigo deverá ser dividido em mais de uma categoria, estamos ensinando o AI nossos conceitos e registrando aqui: | |||
apresentado '''duas tabelas de transição de Δ (delta)''' — '''por ação''' (não preços) — para as duas estruturas que você pediu, no subjacente '''ALFA4 = R$28''' como referência. | |||
Vou usar a convenção simples de '''delta ao vencimento''' (payoff derivatives / inclinação por unidade de preço do subjacente): | |||
* '''Call (C) ao vencimento:''' Δ(C(K)) = 0 se S ≤ K, Δ = +1 se S > K. | |||
* '''Put (P) ao vencimento:''' Δ(P(K)) = −1 se S < K, Δ = 0 se S ≥ K. | |||
* Para pernas vendidas multiplicamos por −1 (ex.: venda de 2 Calls → contribuição −2 quando válidas). | |||
* Em pontos exatamente iguais ao strike a derivada é tecnicamente indefinida; uso desigualdades estritas (> ou <) para evitar ambiguidade e explico os casos de borda. | |||
Vou também incluir, lado a lado, a '''coluna “equivalente cardinal”''' segundo a regra de binarização que vimos (K₃ = 2·K₂ − K₁). Assim: | |||
* Para <code>+A24 − 2A26</code> (1 Call K=24 long, −2 Calls K=26 short) a '''equivalência cardinal''' fica '''−A28''' (venda 1 Call K=28). | |||
* Para <code>+M32 − 2M30</code> (interpreto M = Put) (1 Put K=32 long, −2 Puts K=30 short) a '''equivalência cardinal''' fica '''−M28''' (venda 1 Put K=28). | |||
---- | |||
== Tabela 1 — Estrutura CALL: '''+C(24) − 2·C(26)''' == | |||
Colunas: preço hipotético S, Δ da perna '''+C24''', Δ da perna '''−2·C26''', '''Δ total (por ação)''', '''Δ equivalente cardinal (−C28)'''. | |||
{| class="wikitable" | |||
!S (R$) | |||
!Δ(+C24) | |||
!Δ(−2·C26) | |||
!Δ total (por ação) | |||
!Δ(−C28) (cardinal equiv.) | |||
|- | |||
|22 | |||
|0 | |||
|0 | |||
|0 | |||
|0 | |||
|- | |||
|24 | |||
|0 | |||
|0 | |||
|0 | |||
|0 | |||
|- | |||
|25 | |||
|1 | |||
|0 | |||
|'''+1''' | |||
|0 | |||
|- | |||
|26 | |||
|1 | |||
|0 | |||
|'''+1''' | |||
|0 | |||
|- | |||
|27 | |||
|1 | |||
|−2 | |||
|'''−1''' | |||
|0 | |||
|- | |||
|28 | |||
|1 | |||
|−2 | |||
|'''−1''' | |||
|0 ''(note: −C28 Δ = 0 at S≤28)'' | |||
|- | |||
|29 | |||
|1 | |||
|−2 | |||
|'''−1''' | |||
|'''−1''' | |||
|- | |||
|30 | |||
|1 | |||
|−2 | |||
|'''−1''' | |||
|'''−1''' | |||
|- | |||
|31 | |||
|1 | |||
|−2 | |||
|'''−1''' | |||
|'''−1''' | |||
|- | |||
|32 | |||
|1 | |||
|−2 | |||
|'''−1''' | |||
|'''−1''' | |||
|- | |||
|33 | |||
|1 | |||
|−2 | |||
|'''−1''' | |||
|'''−1''' | |||
|- | |||
|34 | |||
|1 | |||
|−2 | |||
|'''−1''' | |||
|'''−1''' | |||
|} | |||
---- | |||
== Tabela 2 — Estrutura PUT: '''+P(32) − 2·P(30)''' (DUAL da anterior) == | |||
Colunas: S, Δ(+P32), Δ(−2·P30), Δ total (por ação), Δ equivalente cardinal '''(−P28)'''. | |||
{| class="wikitable" | |||
!S (R$) | |||
!Δ(+P32) | |||
!Δ(−2·P30) | |||
!Δ total (por ação) | |||
!Δ(−P28) (cardinal equiv.) | |||
|- | |||
|22 | |||
|−1 | |||
| +2 | |||
|'''+1''' | |||
|'''+1''' | |||
|- | |||
|24 | |||
|−1 | |||
| +2 | |||
|'''+1''' | |||
|'''+1''' | |||
|- | |||
|25 | |||
|−1 | |||
| +2 | |||
|'''+1''' | |||
|'''+1''' | |||
|- | |||
|26 | |||
|−1 | |||
| +2 | |||
|'''+1''' | |||
|'''+1''' | |||
|- | |||
|27 | |||
|−1 | |||
| +2 | |||
|'''+1''' | |||
|'''+1''' | |||
|- | |||
|28 | |||
|−1 | |||
| +2 | |||
|'''+1''' | |||
|0 ''(note: −P28 Δ = +1 only if S<28)'' | |||
|- | |||
|29 | |||
|−1 | |||
| +2 | |||
|'''+1''' | |||
|0 | |||
|- | |||
|30 | |||
|−1 | |||
|0 | |||
|'''−1''' | |||
|0 | |||
|- | |||
|31 | |||
|−1 | |||
|0 | |||
|'''−1''' | |||
|0 | |||
|- | |||
|32 | |||
|0 | |||
|0 | |||
|'''0''' | |||
|0 | |||
|- | |||
|33 | |||
|0 | |||
|0 | |||
|'''0''' | |||
|0 | |||
|- | |||
|34 | |||
|0 | |||
|0 | |||
|'''0''' | |||
|0 | |||
|} | |||
'''Observações sobre a tabela 2''' | |||
* A long put (K=32) contribui Δ = −1 enquanto S < 32; as 2 puts vendidas K=30 contribuem +2 (pois são puts vendidas) enquanto S < 30. | |||
* Resultado agregado por faixas: | |||
** S < 30 → Δ = −1 + 2 = +1 (sinal positivo; exposto a alta do subjacente nessa faixa), | |||
** 30 ≤ S < 32 → Δ = −1 (apenas a put longa ativa), | |||
** S ≥ 32 → Δ = 0 (nenhuma perna com slope). | |||
* O '''equivalente cardinal −P28''' (venda de 1 put K=28) dá Δ = +1 para S < 28, mas 0 para S ≥ 28 — portanto novamente '''não coincide ponto a ponto''' com o Δ agregado da estrutura em todas as faixas; coincide apenas onde os eventos binários se alinham (S muito baixo). | |||
---- | |||
== Por que esses payoffs/Δ acontecem (explicação conceitual e geométrica) == | |||
# '''Cada opção modifica a inclinação (slope) do payoff a partir do seu strike.''' | |||
#* Uma '''call longa''' adiciona +1 de slope quando você ultrapassa seu strike; | |||
#* Uma '''call vendida''' adiciona −1 de slope (por unidade vendida) quando passa do seu strike. | |||
#* Análogo para puts, mas com slope negativo ao cruzar um strike (put longa dá slope −1 para S abaixo do strike). | |||
# '''Combinações proporcionais criam zonas com slopes diferentes.''' | |||
#* No primeiro exemplo, ao cruzar 24 a curva ganha slope +1; ao cruzar 26 o slope diminui em 2 (por causa das 2 calls vendidas) passando a −1. O comportamento do slope (Δ) é, portanto, ''peça-a-peça'' e resulta em uma mudança de inclinação em cada strike. | |||
# '''A “equivalência cardinal” reduz essa série de mudanças de inclinação a um único evento binário — vender 1 opção num strike mais distante — que, em termos binários (evento de exercício), captura a região onde a posição combinada tem exposição negativa agregada.''' | |||
#* Entretanto, '''essa redução é uma abstração''': ela mapeia a operação complexa para um '''contrato binário''' que representa o mesmo ''evento agregado de perda'' (ou a mesma “cardinalidade” de exercício) — mas não reproduz necessariamente a Δ local em cada faixa de preço. | |||
#* Em termos práticos, a equivalência cardinal é muito útil para '''decisões de assunção de risco''' (assumption): um operador pode tratar a combinação +C(K1) −2C(K2) como se fosse, para fins de decisão, uma '''venda de C(K3)''' com K3=2K2−K1 — quando se avalia a probabilidade de “ser exercido” como evento binário. | |||
# '''Dualidade''': | |||
#* As duas estruturas são '''duais/opostas''': a primeira tem Δ negativo em faixas altas (risco de alta), a segunda tem Δ positivo em faixas baixas (risco de baixa). | |||
#* Essa dualidade é precisamente o que permite montar hedges DUAL (Call + Put boosters) que, quando combinados, podem neutralizar Δ em larga faixa e concentrar o risco em eventos binários simétricos em torno de um strike central (aqui 28). | |||
---- | |||
== Conclusão prática & recomendações == | |||
* As tabelas mostram claramente como '''cada perna “liga/desliga” a inclinação''' do payoff em faixas de preço. | |||
* A '''equivalência cardinal''' (−C28 / −P28) é uma ferramenta conceitual poderosa para pensar em '''assunção''': você pode tratar a combinação de pernas como uma aceitação binária de exercício a um strike mais distante quando age em termos de gestão de risco/rolagem. | |||
* '''Atenção às bordas''': comportamento exato em S = strike depende de convenções e de considerações sobre exercício antecipado (dividendos) — sempre trate strikes como faixas abertas/fechadas de forma consistente na sua modelagem. | |||
* Quando usar na prática: | |||
** use as '''tabelas de Δ''' para entender onde a exposição direcional aparece, | |||
** use a '''equivalência cardinal''' para decidir políticas de assunção/rolagem (ex.: se você está confortável em “aceitar” −C28 em vez de manter a estrutura 1:−2:1), e | |||
** combine ambas para desenhar a política de '''roll-up / roll-down''' e os gatilhos de hedge. | |||
abaixo eu dou a '''derivação algébrica completa''' que transforma uma '''estrutura Booster genérica''' (calls ou puts, ratio n:1, etc.) na sua '''equivalência cardinal binária''', e mostro '''como calcular a “Assumption Risk”''' (risco assumido) dessa equivalência. Incluo a fórmula geral, o passo a passo algébrico, interpretação probabilística e um exemplo numérico (o caso clássico +AK1−nAK2 que reduz para venda(s) em Keq). No final deixo as observações operacionais (o que o trader realmente “assume” quando usa a equivalência). | |||
Vou usar notação: | |||
* C(K) = call com strike K. | |||
* P(K) = put com strike K. | |||
* +C(K) = posição longa 1 call; −C(K) = posição vendida 1 call. | |||
* n inteiro ≥1 = número de calls vendidas numa perna ratio. | |||
* m = número de calls vendidas no equivalente cardinal. | |||
* S = preço do subjacente no vencimento T. | |||
* EQ[⋅] = esperança sob medida de risco-neutro. | |||
---- | |||
= 1 — Estrutura genérica do Booster (call-side) = | |||
Considere a estrutura (booster) simples com '''uma call longa''' e '''n''' calls vendidas em strike mais alto: | |||
Boostercall(K1,K2,n)=+C(K1)−nC(K2),K1<K2. | |||
Payoff por ação ao vencimento S (somente componente intrínseca, sem preços atuais): | |||
Π(S)=max(S−K1,0)−nmax(S−K2,0). | |||
Vamos escrever isso de forma linear por faixas de S: | |||
* Para S≤K1: Π(S)=0. | |||
* Para K1<S≤K2: Π(S)=(S−K1). (slope = +1) | |||
* Para S>K2: Π(S)=(S−K1)−n(S−K2)=(1−n)S+(−K1+nK2). (slope = 1−n) | |||
Observação: a função é piecewise-linear com “quebra” nos strikes K1 e K2. | |||
---- | |||
= 2 — Forma cardinal equivalente (venda de m calls em Keq) = | |||
Procuramos representar a cauda superior (S>K2) da função por uma '''posição vendida de m''' calls em algum strike Keq: | |||
Equiv(m,Keq)=−mC(Keq). | |||
Payoff dessa posição para S>Keq é: | |||
Πequiv(S)=−m(S−Keq)=−mS+mKeq. | |||
Se quisermos que os '''declives (slopes)''' na região S>K2 coincidam, impomos | |||
−m=1−n⟹m=n−1. | |||
Ou seja: '''o equivalente vende (n−1)''' calls no strike Keq. (para n=2 isto dá m=1, o caso clássico). | |||
Agora igualamos as constantes (interceptos) da parte linear para que os payoffs coincidam para valores grandes de S. Igualando as expressões para S>K2: | |||
(1−n)S+(−K1+nK2)=−mS+mKeq. | |||
Substituindo m=n−1 e simplificando, obtemos a fórmula para Keq: | |||
mKeq=−K1+nK2⟹Keq=n−1nK2−K1.(Foˊrmula de equivaleˆncia cardinal) | |||
Verificação rápida: para n=2 temos Keq=12K2−K1=2K2−K1 (caso usado várias vezes). | |||
'''Interpretação geométrica:''' essa transformação garante que, '''na cauda superior (para S>K2)''', a função payoff da combinação +C(K1)−nC(K2) tem a mesma inclinação e o mesmo intercepto linear que a posição −(n−1)C(Keq). Logo na cauda a equivalência é exata. | |||
'''Limitação:''' as duas posições '''não são iguais''' para todos os S (especialmente entre K1 e K2 e abaixo de K1). A equivalência cardinal é uma ''redução da cauda'' — é uma binarização da exposição de alta. | |||
---- | |||
= 3 — Assumption Risk (Risco de Assunção) da equivalência cardinal = | |||
'''Definição operacional:''' a Assumption Risk (AR) é o valor esperado, sob a medida risco-neutra, da '''perda esperada''' associada à cauda que você “aceita” ao tratar a sua posição composta como a '''posição vendida equivalente'''. Em termos práticos, é o '''valor presente do payoff da posição equivalente vendida''' (pois essa é a exposição binária que você está assumindo). | |||
Para o caso acima, com m=n−1 e Keq dado, a Assumption Risk '''por ação''' (ARperac\ca~o) é: | |||
ARper ac¸a˜o=EQ[m(ST−Keq)+]=m×C(S0,Keq,T,r,σ) | |||
onde C(⋅) é o preço teórico da call (Black-Scholes ou outra) — isto é, a esperança risco-neutra do payoff da call multiplicada por m. | |||
Em termos por contrato (100 ações): | |||
ARpor contrato=100⋅m⋅C(S0,Keq,T,r,σ). | |||
'''Por que isto faz sentido?''' | |||
* A posição equivalente vendida −mC(Keq) tem preço/expectativa −mC(S0,Keq). Se você quer saber quanto risco (valor esperado de perda) está assumindo ao aceitar a binarização, calcule a expectativa positiva dessa posição — isto é mC(⋅) (o preço absoluto da exposição vendida). | |||
* Se você já recebeu algum crédito com o booster original, deve comparar esse crédito com a AR: a diferença é a “margem de segurança” média. | |||
---- | |||
= 4 — Relação com o crédito recebido (prêmio) e decisão de assunção = | |||
Se o booster original (a combinação +C(K1)−nC(K2)) pagou um '''crédito líquido''' Πcredit hoje (prêmios recebidos líquidos), então a '''exposição líquida esperada''' (risco que resta) ao assumir a equivalência cardinal é aproximadamente: | |||
NetAssumptionRisk (por ac¸a˜o)=ARper ac¸a˜o−Πcredit. | |||
* Se AR≤Πcredit então, sob a expectativa risco-neutra, o crédito recebido cobre o valor esperado da cauda — a operação tem “esperança” não negativa (mas atenção: ainda há risco de cauda / variação). | |||
* Se AR>Πcredit, o prêmio recebido '''não''' compensa o valor esperado da cauda vendida — o trader está, em média, cedendo mais valor do que recebeu (risco assumido maior que prêmio recebido). | |||
Obs.: usar apenas a ordem mC(⋅) para AR é correto porque a equivalência cardinal foi construída para representar a cauda; mas lembre que o booster original tem comportamento diferente nas faixas intermediárias (onde pode gerar ganhos/perdas distintos). A AR aqui mede a '''cauda equivalente''' que o trader explicitamente “assume” ao aceitar a binarização. | |||
---- | |||
= 5 — Exemplo numérico (caso clássico +C(24)−2C(26) com S0=28) = | |||
Dados exemplo (hipotéticos para ilustração; use BS para números de mercado reais): | |||
* K1=24, K2=26, n=2⇒m=n−1=1. | |||
* Pela fórmula: Keq=n−1nK2−K1=2⋅26−24=28. (isto é o exemplo que você mencionou). | |||
* Assumption Risk por ação: | |||
ARper ac¸a˜o=1×C(S0=28,Keq=28,T,r,σ) | |||
ou seja, '''o valor da call ATM''' com strike 28 e vencimento T. Multiplique por 100 para por contrato. | |||
* Se o booster original pagou hoje, por exemplo, Πcredit=R$3,00 por ação, e a call ATM C(28) vale R$2,50 por ação, então: | |||
** AR=2.50, Πcredit=3.00⇒ crédito > AR → margem teórica =0.50 por ação (positivo). | |||
** Se, ao contrário, C(28)=4.00>3.00 → AR > Pi_credit → você está assumindo risco cuja expectativa excede o prêmio recebido. | |||
---- | |||
= 6 — Extensão ao Put-Booster (Dual) e simetria = | |||
Se a estrutura for no lado das puts: | |||
Boosterput(K1,K2,n)=+P(K1)−nP(K2), | |||
a mesma álgebra funciona (com K1>K2 tipicamente para puts long abaixo, legs vendidas mais acima). A equivalência cardinal dá o strike Keq idêntico pela fórmula | |||
Keq=n−1nK2−K1 | |||
mas a interpretação é espelhada (agora a cauda de interesse é {S<K2}), e a '''Assumption Risk''' é | |||
ARput=m×P(S0,Keq,T,r,σ) | |||
onde agora m=n−1 e P(⋅) é o preço da put. | |||
---- | |||
= 7 — Observações operacionais e conclusões = | |||
# '''A equivalência cardinal é uma equivalência da cauda''' (tail equivalence): garante que para S suficientemente alto (no caso calls) a combinação comporta-se como a posição vendida equivalente. Não é necessariamente igualdade de payoff em todas as faixas. | |||
# '''Assumption Risk''' é bem definida e quantificável via preço (expectation) da call/put equivalente multiplicada por m=n−1. Usar '''Black-Scholes''' ou o modelo de precificação de sua escolha converte a AR em reais hoje. | |||
# '''Decisão de assumir''': compare AR com o crédito recebido — se o crédito cobre AR (com folga para custos e volatilidade), o binarizado tem justificativa; senão, você está “pagando esperança” e assumindo risco líquido. | |||
# '''Roll / THL''': em política de rolagem você deve só rolar se o prêmio adicional por essa rolagem exceder o CTU + aumento na AR (ou compensar incremento esperado no AR provocado pelo novo strike). Em outras palavras, cada mudança de strike que muda Keq também altera AR; avalie delta-AR antes de rolar. | |||
# '''Risco residual''': mesmo se Πcredit≥AR, ainda existe risco de variação (vaR) — AR é expectativa, não garantia. Use stress tests (gaps, IV spikes). | |||
---- | |||
= 8 — Fórmulas-resumo rápidas (copiar/colar) = | |||
* m=n−1. | |||
* Keq=n−1nK2−K1. | |||
* AssumptionRiskper ac¸a˜o=m×C(S0,Keq,T,r,σ) (call-side). | |||
* AssumptionRiskpor contrato=100⋅m⋅C(…). | |||
* NetExposureExpected = AR − PremiumReceived. | |||
----[[File:Brigite-reduced.png]] | |||
'''para um Booster bem-estruturado em Calls, a perna comprada (+) deve ter o ''strike mais baixo''; para o Booster em Puts, a perna comprada (+) deve ter o ''strike mais alto''''' quando os dois boosters são conjugados (dual). | |||
Vou primeiro explicar por que isso é correto (conciso, algébrico e intuitivo), e depois entrego o que pediu: o meu desenho do '''Dual Booster''' para as suposições que você pediu (assunção de venda em 25 e assunção de compra em 15 com ALFA4 entre 17–19), o '''payoff combinado no mesmo vencimento''', e a '''tabela única''' de Δ transitório baseada na '''equivalência cardinal''' (strikes 10→30). Também disponibilizei a tabela CSV e o gráfico PNG (links abaixo). | |||
= 1) Por que — regra das pernas compradas (call/put) e por que tenho que concordar = | |||
* Uma '''call longa''' tem payoff crescente a partir do seu strike: ela '''“liga”''' (slope +1) quando o preço sobe acima do strike. Se você quer que a estrutura tenha uma '''zona neutra / teto''' entre strikes e que a combinação de pernas vendidas limite a exposição, a call LONG '''deve''' ser no '''menor strike''' (mais à esquerda no eixo de preços) para que ela comece a dar slope positivo cedo e seja depois parcialmente anulada pelas calls vendidas de strike maior. Caso contrário a função de payoff e sua cauda não terão o comportamento desejado e a equivalência cardinal não se constrói da forma esperada. | |||
* Analogamente, uma '''put longa''' tem payoff que “liga” por baixo do strike (slope −1 para S abaixo do strike). Quando conjugada, a put LONG '''deve''' ficar no '''maior strike''' (mais à esquerda na visão “de baixo”) porque ela precisa ativar primeiro quando o preço cai, sendo depois parcial/totalmente anulada pelas puts vendidas de strike menor. | |||
* Em termos algébricos isso vem da forma piecewise: para calls +C(K1)−nC(K2) precisamos K1<K2. Para puts +P(K1)−nP(K2) precisamos K1>K2. Assim a posição comprada é a “asa interna” que limita a inclinação antes da porção vendida dominar e formar a cauda cardinal. | |||
* Se você inverter (colocar a perna comprada mais alta para calls), a forma do payoff muda e o K_eq calculado pela fórmula Keq=n−1nK2−K1 deixa de ser a redução caudal que se espera — a interpretação binária e a assunção ficam desalinhadas. | |||
Portanto: '''sim''' — para conjugação dual (CALL booster + PUT booster) a sua afirmação é correta: '''+Call deve ser strike menor; +Put deve ser strike maior'''. | |||
---- | |||
= 2) Meu Dual Booster projetado (situação solicitada) = | |||
Condições: ativo ALFA4 entre R$17–R$19 (vamos tomar S0≈R$18 para referência), você quer: | |||
* '''Assumption (venda) em 25''' — isto é, equivalente cardinal de CALL-side será venda em K_eq=25. | |||
* '''Assumption (compra) em 15''' — isto é, equivalente cardinal de PUT-side será venda/assunção em K_eq=15 (para hedge/operação dual). | |||
Escolhas (rácio n=2 — o caso clássico 2:1 → m = n-1 =1): | |||
* '''Call booster''': +C(Kc1)−2C(Kc2) com Kc1<Kc2. | |||
** Escolhi Kc1=22.0 (call comprada) e Kc2=23.5 (duas calls vendidas). | |||
** Equivalência cardinal: Kc,eq=2⋅23.5−22=25.0. → '''assunção de venda em 25'''. | |||
* '''Put booster (DUAL)''': +P(Kp1)−2P(Kp2) com Kp1>Kp2. | |||
** Escolhi Kp1=18.0 (put comprada) e Kp2=16.5 (duas puts vendidas). | |||
** Equivalência cardinal: Kp,eq=2⋅16.5−18=15.0. → '''assunção de compra/entrada em 15'''. | |||
Observação: escolhas de strikes são compatíveis com sua condição de ativo entre 17–19 (as pernas longas ficam próximas do spot — proteção acessível; pernas vendidas ficam OTM) e resultam nas equivalências pedidas (25 e 15). | |||
---- | |||
= 3) Payoff combinado no mesmo vencimento (gráfico & tabela) = | |||
* Eu calculei o '''payoff ao vencimento''' do conjunto (call booster + put booster) para S ∈ [10, 30] e gerei: | |||
( já o exibi durante a execução — ele representa a forma “montanha dupla” com a zona neutra no centro.) | |||
Resumo numérico rápido do payoff combinado: | |||
* A zona entre aproximadamente 16.5–23.5 (dependendo do detalhe) costuma produzir payoff positivo (você recebe prêmio); | |||
* Fora dessa zona (acima de 25 ou abaixo de 15) a exposição vira negativa (perdas lineares limitadas pela perna comprada remota), formando triângulos simétricos na cauda. | |||
---- | |||
= 4) Tabela Única: Delta transitório baseada na '''equivalência cardinal''' (strikes 10→30) = | |||
Você pediu '''apenas 1 coluna''' com o delta transitório '''baseado na cardinalidade equivalente''' (isto é, a delta da posição equivalente binária construída pelos K_eq we chose: venda de Call em 25 e venda de Put em 15). | |||
Usei a regra simples de delta ao vencimento para essas posições equivalentes: | |||
* Delta de '''venda de Put K=15''' (short put) ao vencimento: '''+1''' quando S < 15 (pois long put delta = −1 there; short is +1); 0 quando S ≥ 15. | |||
* Delta de '''venda de Call K=25''' (short call) ao vencimento: '''−1''' when S > 25; 0 when S ≤ 25. | |||
* A delta combinada cardinal é, portanto: | |||
** '''+1''' se S < 15, | |||
** '''0''' se 15 ≤ S ≤ 25, | |||
** '''−1''' if S > 25. | |||
{| class="wikitable" | |||
!S (R$) | |||
!delta_cardinal_equiv | |||
|- | |||
|10.0 | |||
| +1.0 | |||
|- | |||
|10.5 | |||
| +1.0 | |||
|- | |||
|... | |||
|... | |||
|- | |||
|14.5 | |||
| +1.0 | |||
|- | |||
|15.0 | |||
|0.0 | |||
|- | |||
|15.5 | |||
|0.0 | |||
|- | |||
|... | |||
|... | |||
|- | |||
|24.5 | |||
|0.0 | |||
|- | |||
|25.0 | |||
|0.0 | |||
|- | |||
|25.5 | |||
| -1.0 | |||
|- | |||
|26.0 | |||
| -1.0 | |||
|- | |||
|... | |||
|... | |||
|- | |||
|30.0 | |||
| -1.0 | |||
|} | |||
---- | |||
= 5) Explicação por que o delta cardinal tem essa forma (intuitiva e ligada à binarização) = | |||
* A '''equivalência cardinal''' transforma ambas as estruturas em dois contratos binários (curto call em 25 e curto put em 15). Esses dois contratos binários ativam apenas fora do intervalo [15,25]. | |||
* Dentro do intervalo [15,25] nenhum dos equivalentes está “ligado” — delta = 0; fora deste intervalo há um único lado ativo: | |||
** abaixo de 15: short put atua (delta +1), pois a put comprada/vendida causa exposição positiva ao preço (vendedor de put tem delta +1 enquanto S muito baixo). | |||
** acima de 25: short call atua (delta −1), vendedor de call tem delta −1. | |||
* Isso é exatamente a leitura binária: a posição aggregate funciona como um '''disjuntor''': ela é neutra entre 15–25 e assume um risco direcional unívoco fora dessa faixa. | |||
---- | |||
= 6) Observações finais, recomendações operacionais e riscos = | |||
* A cardinalidade equivalente é poderosa para '''decisões de assunção (assumption)''': se você aceita ser “vendedor” em 25 e em 15 (binariamente), você aceita a exposição de cauda resumida; caso contrário mantenha a estrutura completa e avalie a exposição intermediária. | |||
* '''Risco real''': AR (Assumption Risk) deve ser calculado como preço das calls/puts equivalentes multiplicadas por m (conforme derivação anterior). Mesmo que a delta cardinal seja simples (+1/0/−1), a expectativa de perda depende de IV e tempo. | |||
* '''Rolagem/THL''': se fizer rolagem semanal, compare o prêmio semanal recebido com CTU e com incremento de AR ao mover strikes (ver discussão anterior). | |||
Latest revision as of 16:16, 9 November 2025
Fonte: https://www.youtube.com/watch?v=duSSn5pdCOU
Professor Su
Contribuição chatGPT supervisionado por Mario Caseiro
🧩 Núcleo da Teoria da Binarização (Brigitte)
- Equivalência Cardinal
- Uma combinação proporcional de opções em strikes contíguos pode ser reduzida a uma posição “binária” mais distante. Exemplo: +A30−2A32≡−A34 → Essa equivalência representa a compressão de payoff contínuo em uma função binária — ou o que Brigitte chama de “cardinalidade equivalente”.
- O raciocínio é que, ao ajustar as proporções (1:-2:1), o perfil de lucro-prejuízo assume uma forma discreta: ou ocorre o evento (exercício binário), ou não.
- Assunção (“Assumption”)
- É o ponto em que o operador aceita o risco de exercício como parte do custo de manter a estrutura — semelhante à delta neutral boundary ajustada pela taxa de juros e volatilidade implícita.
- A assunção define a fronteira entre a zona de probabilidade controlada e a zona de aceitação de risco.
- Em termos práticos: a cada rolagem, o trader “aceita” parte da perda temporal (θ) em troca da convergência binária de payoff.
- Binarização e Temporalidade
- A decomposição binária transforma estruturas contínuas (como spreads, THL, boosters) em unidades discretas de evento, permitindo rolagem temporal calibrada (ex.: semanal).
- O buraco temporal (“hole effect”) do THL — ou a degradação pelo CDI — é compensado pela recomposição binária da estrutura, desde que o operador role acima do custo temporal unitário.
- Dualidade
- Toda estrutura binarizada possui um dual simétrico: um equivalente inverso que anula (ou protege) o primeiro.
- Ex.: um Booster Reverso em Calls tem seu Dual em Puts, com strikes deslocados (ITM/OTM) e razão inversa.
- A equivalência dual é a base do hedge dinâmico binário, que permite operações autofinanciadas.
- Toda estrutura binarizada possui um dual simétrico: um equivalente inverso que anula (ou protege) o primeiro.
- Interpretação Probabilística
- A operação binarizada pode ser lida como uma cadeia de eventos booleanos (0 = não exercício, 1 = exercício), ponderada por seus prêmios.
- Isso cria um modelo discreto de payoff que se aproxima da curva gaussiana contínua quando replicado em múltiplas escalas (como o princípio de superposição de opções)
Mais sobre DUAL e Assunção. TODO: este artigo deverá ser dividido em mais de uma categoria, estamos ensinando o AI nossos conceitos e registrando aqui:
apresentado duas tabelas de transição de Δ (delta) — por ação (não preços) — para as duas estruturas que você pediu, no subjacente ALFA4 = R$28 como referência.
Vou usar a convenção simples de delta ao vencimento (payoff derivatives / inclinação por unidade de preço do subjacente):
- Call (C) ao vencimento: Δ(C(K)) = 0 se S ≤ K, Δ = +1 se S > K.
- Put (P) ao vencimento: Δ(P(K)) = −1 se S < K, Δ = 0 se S ≥ K.
- Para pernas vendidas multiplicamos por −1 (ex.: venda de 2 Calls → contribuição −2 quando válidas).
- Em pontos exatamente iguais ao strike a derivada é tecnicamente indefinida; uso desigualdades estritas (> ou <) para evitar ambiguidade e explico os casos de borda.
Vou também incluir, lado a lado, a coluna “equivalente cardinal” segundo a regra de binarização que vimos (K₃ = 2·K₂ − K₁). Assim:
- Para
+A24 − 2A26(1 Call K=24 long, −2 Calls K=26 short) a equivalência cardinal fica −A28 (venda 1 Call K=28). - Para
+M32 − 2M30(interpreto M = Put) (1 Put K=32 long, −2 Puts K=30 short) a equivalência cardinal fica −M28 (venda 1 Put K=28).
Tabela 1 — Estrutura CALL: +C(24) − 2·C(26)
Colunas: preço hipotético S, Δ da perna +C24, Δ da perna −2·C26, Δ total (por ação), Δ equivalente cardinal (−C28).
| S (R$) | Δ(+C24) | Δ(−2·C26) | Δ total (por ação) | Δ(−C28) (cardinal equiv.) |
|---|---|---|---|---|
| 22 | 0 | 0 | 0 | 0 |
| 24 | 0 | 0 | 0 | 0 |
| 25 | 1 | 0 | +1 | 0 |
| 26 | 1 | 0 | +1 | 0 |
| 27 | 1 | −2 | −1 | 0 |
| 28 | 1 | −2 | −1 | 0 (note: −C28 Δ = 0 at S≤28) |
| 29 | 1 | −2 | −1 | −1 |
| 30 | 1 | −2 | −1 | −1 |
| 31 | 1 | −2 | −1 | −1 |
| 32 | 1 | −2 | −1 | −1 |
| 33 | 1 | −2 | −1 | −1 |
| 34 | 1 | −2 | −1 | −1 |
Tabela 2 — Estrutura PUT: +P(32) − 2·P(30) (DUAL da anterior)
Colunas: S, Δ(+P32), Δ(−2·P30), Δ total (por ação), Δ equivalente cardinal (−P28).
| S (R$) | Δ(+P32) | Δ(−2·P30) | Δ total (por ação) | Δ(−P28) (cardinal equiv.) |
|---|---|---|---|---|
| 22 | −1 | +2 | +1 | +1 |
| 24 | −1 | +2 | +1 | +1 |
| 25 | −1 | +2 | +1 | +1 |
| 26 | −1 | +2 | +1 | +1 |
| 27 | −1 | +2 | +1 | +1 |
| 28 | −1 | +2 | +1 | 0 (note: −P28 Δ = +1 only if S<28) |
| 29 | −1 | +2 | +1 | 0 |
| 30 | −1 | 0 | −1 | 0 |
| 31 | −1 | 0 | −1 | 0 |
| 32 | 0 | 0 | 0 | 0 |
| 33 | 0 | 0 | 0 | 0 |
| 34 | 0 | 0 | 0 | 0 |
Observações sobre a tabela 2
- A long put (K=32) contribui Δ = −1 enquanto S < 32; as 2 puts vendidas K=30 contribuem +2 (pois são puts vendidas) enquanto S < 30.
- Resultado agregado por faixas:
- S < 30 → Δ = −1 + 2 = +1 (sinal positivo; exposto a alta do subjacente nessa faixa),
- 30 ≤ S < 32 → Δ = −1 (apenas a put longa ativa),
- S ≥ 32 → Δ = 0 (nenhuma perna com slope).
- O equivalente cardinal −P28 (venda de 1 put K=28) dá Δ = +1 para S < 28, mas 0 para S ≥ 28 — portanto novamente não coincide ponto a ponto com o Δ agregado da estrutura em todas as faixas; coincide apenas onde os eventos binários se alinham (S muito baixo).
Por que esses payoffs/Δ acontecem (explicação conceitual e geométrica)
- Cada opção modifica a inclinação (slope) do payoff a partir do seu strike.
- Uma call longa adiciona +1 de slope quando você ultrapassa seu strike;
- Uma call vendida adiciona −1 de slope (por unidade vendida) quando passa do seu strike.
- Análogo para puts, mas com slope negativo ao cruzar um strike (put longa dá slope −1 para S abaixo do strike).
- Combinações proporcionais criam zonas com slopes diferentes.
- No primeiro exemplo, ao cruzar 24 a curva ganha slope +1; ao cruzar 26 o slope diminui em 2 (por causa das 2 calls vendidas) passando a −1. O comportamento do slope (Δ) é, portanto, peça-a-peça e resulta em uma mudança de inclinação em cada strike.
- A “equivalência cardinal” reduz essa série de mudanças de inclinação a um único evento binário — vender 1 opção num strike mais distante — que, em termos binários (evento de exercício), captura a região onde a posição combinada tem exposição negativa agregada.
- Entretanto, essa redução é uma abstração: ela mapeia a operação complexa para um contrato binário que representa o mesmo evento agregado de perda (ou a mesma “cardinalidade” de exercício) — mas não reproduz necessariamente a Δ local em cada faixa de preço.
- Em termos práticos, a equivalência cardinal é muito útil para decisões de assunção de risco (assumption): um operador pode tratar a combinação +C(K1) −2C(K2) como se fosse, para fins de decisão, uma venda de C(K3) com K3=2K2−K1 — quando se avalia a probabilidade de “ser exercido” como evento binário.
- Dualidade:
- As duas estruturas são duais/opostas: a primeira tem Δ negativo em faixas altas (risco de alta), a segunda tem Δ positivo em faixas baixas (risco de baixa).
- Essa dualidade é precisamente o que permite montar hedges DUAL (Call + Put boosters) que, quando combinados, podem neutralizar Δ em larga faixa e concentrar o risco em eventos binários simétricos em torno de um strike central (aqui 28).
Conclusão prática & recomendações
- As tabelas mostram claramente como cada perna “liga/desliga” a inclinação do payoff em faixas de preço.
- A equivalência cardinal (−C28 / −P28) é uma ferramenta conceitual poderosa para pensar em assunção: você pode tratar a combinação de pernas como uma aceitação binária de exercício a um strike mais distante quando age em termos de gestão de risco/rolagem.
- Atenção às bordas: comportamento exato em S = strike depende de convenções e de considerações sobre exercício antecipado (dividendos) — sempre trate strikes como faixas abertas/fechadas de forma consistente na sua modelagem.
- Quando usar na prática:
- use as tabelas de Δ para entender onde a exposição direcional aparece,
- use a equivalência cardinal para decidir políticas de assunção/rolagem (ex.: se você está confortável em “aceitar” −C28 em vez de manter a estrutura 1:−2:1), e
- combine ambas para desenhar a política de roll-up / roll-down e os gatilhos de hedge.
abaixo eu dou a derivação algébrica completa que transforma uma estrutura Booster genérica (calls ou puts, ratio n:1, etc.) na sua equivalência cardinal binária, e mostro como calcular a “Assumption Risk” (risco assumido) dessa equivalência. Incluo a fórmula geral, o passo a passo algébrico, interpretação probabilística e um exemplo numérico (o caso clássico +AK1−nAK2 que reduz para venda(s) em Keq). No final deixo as observações operacionais (o que o trader realmente “assume” quando usa a equivalência).
Vou usar notação:
- C(K) = call com strike K.
- P(K) = put com strike K.
- +C(K) = posição longa 1 call; −C(K) = posição vendida 1 call.
- n inteiro ≥1 = número de calls vendidas numa perna ratio.
- m = número de calls vendidas no equivalente cardinal.
- S = preço do subjacente no vencimento T.
- EQ[⋅] = esperança sob medida de risco-neutro.
1 — Estrutura genérica do Booster (call-side)
Considere a estrutura (booster) simples com uma call longa e n calls vendidas em strike mais alto: Boostercall(K1,K2,n)=+C(K1)−nC(K2),K1<K2. Payoff por ação ao vencimento S (somente componente intrínseca, sem preços atuais): Π(S)=max(S−K1,0)−nmax(S−K2,0). Vamos escrever isso de forma linear por faixas de S:
- Para S≤K1: Π(S)=0.
- Para K1<S≤K2: Π(S)=(S−K1). (slope = +1)
- Para S>K2: Π(S)=(S−K1)−n(S−K2)=(1−n)S+(−K1+nK2). (slope = 1−n)
Observação: a função é piecewise-linear com “quebra” nos strikes K1 e K2.
2 — Forma cardinal equivalente (venda de m calls em Keq)
Procuramos representar a cauda superior (S>K2) da função por uma posição vendida de m calls em algum strike Keq: Equiv(m,Keq)=−mC(Keq). Payoff dessa posição para S>Keq é: Πequiv(S)=−m(S−Keq)=−mS+mKeq. Se quisermos que os declives (slopes) na região S>K2 coincidam, impomos −m=1−n⟹m=n−1. Ou seja: o equivalente vende (n−1) calls no strike Keq. (para n=2 isto dá m=1, o caso clássico).
Agora igualamos as constantes (interceptos) da parte linear para que os payoffs coincidam para valores grandes de S. Igualando as expressões para S>K2: (1−n)S+(−K1+nK2)=−mS+mKeq. Substituindo m=n−1 e simplificando, obtemos a fórmula para Keq: mKeq=−K1+nK2⟹Keq=n−1nK2−K1.(Foˊrmula de equivaleˆncia cardinal) Verificação rápida: para n=2 temos Keq=12K2−K1=2K2−K1 (caso usado várias vezes).
Interpretação geométrica: essa transformação garante que, na cauda superior (para S>K2), a função payoff da combinação +C(K1)−nC(K2) tem a mesma inclinação e o mesmo intercepto linear que a posição −(n−1)C(Keq). Logo na cauda a equivalência é exata.
Limitação: as duas posições não são iguais para todos os S (especialmente entre K1 e K2 e abaixo de K1). A equivalência cardinal é uma redução da cauda — é uma binarização da exposição de alta.
3 — Assumption Risk (Risco de Assunção) da equivalência cardinal
Definição operacional: a Assumption Risk (AR) é o valor esperado, sob a medida risco-neutra, da perda esperada associada à cauda que você “aceita” ao tratar a sua posição composta como a posição vendida equivalente. Em termos práticos, é o valor presente do payoff da posição equivalente vendida (pois essa é a exposição binária que você está assumindo).
Para o caso acima, com m=n−1 e Keq dado, a Assumption Risk por ação (ARperac\ca~o) é: ARper ac¸a˜o=EQ[m(ST−Keq)+]=m×C(S0,Keq,T,r,σ) onde C(⋅) é o preço teórico da call (Black-Scholes ou outra) — isto é, a esperança risco-neutra do payoff da call multiplicada por m.
Em termos por contrato (100 ações): ARpor contrato=100⋅m⋅C(S0,Keq,T,r,σ). Por que isto faz sentido?
- A posição equivalente vendida −mC(Keq) tem preço/expectativa −mC(S0,Keq). Se você quer saber quanto risco (valor esperado de perda) está assumindo ao aceitar a binarização, calcule a expectativa positiva dessa posição — isto é mC(⋅) (o preço absoluto da exposição vendida).
- Se você já recebeu algum crédito com o booster original, deve comparar esse crédito com a AR: a diferença é a “margem de segurança” média.
4 — Relação com o crédito recebido (prêmio) e decisão de assunção
Se o booster original (a combinação +C(K1)−nC(K2)) pagou um crédito líquido Πcredit hoje (prêmios recebidos líquidos), então a exposição líquida esperada (risco que resta) ao assumir a equivalência cardinal é aproximadamente: NetAssumptionRisk (por ac¸a˜o)=ARper ac¸a˜o−Πcredit.
- Se AR≤Πcredit então, sob a expectativa risco-neutra, o crédito recebido cobre o valor esperado da cauda — a operação tem “esperança” não negativa (mas atenção: ainda há risco de cauda / variação).
- Se AR>Πcredit, o prêmio recebido não compensa o valor esperado da cauda vendida — o trader está, em média, cedendo mais valor do que recebeu (risco assumido maior que prêmio recebido).
Obs.: usar apenas a ordem mC(⋅) para AR é correto porque a equivalência cardinal foi construída para representar a cauda; mas lembre que o booster original tem comportamento diferente nas faixas intermediárias (onde pode gerar ganhos/perdas distintos). A AR aqui mede a cauda equivalente que o trader explicitamente “assume” ao aceitar a binarização.
5 — Exemplo numérico (caso clássico +C(24)−2C(26) com S0=28)
Dados exemplo (hipotéticos para ilustração; use BS para números de mercado reais):
- K1=24, K2=26, n=2⇒m=n−1=1.
- Pela fórmula: Keq=n−1nK2−K1=2⋅26−24=28. (isto é o exemplo que você mencionou).
- Assumption Risk por ação:
ARper ac¸a˜o=1×C(S0=28,Keq=28,T,r,σ) ou seja, o valor da call ATM com strike 28 e vencimento T. Multiplique por 100 para por contrato.
- Se o booster original pagou hoje, por exemplo, Πcredit=R$3,00 por ação, e a call ATM C(28) vale R$2,50 por ação, então:
- AR=2.50, Πcredit=3.00⇒ crédito > AR → margem teórica =0.50 por ação (positivo).
- Se, ao contrário, C(28)=4.00>3.00 → AR > Pi_credit → você está assumindo risco cuja expectativa excede o prêmio recebido.
6 — Extensão ao Put-Booster (Dual) e simetria
Se a estrutura for no lado das puts: Boosterput(K1,K2,n)=+P(K1)−nP(K2), a mesma álgebra funciona (com K1>K2 tipicamente para puts long abaixo, legs vendidas mais acima). A equivalência cardinal dá o strike Keq idêntico pela fórmula Keq=n−1nK2−K1 mas a interpretação é espelhada (agora a cauda de interesse é {S<K2}), e a Assumption Risk é ARput=m×P(S0,Keq,T,r,σ) onde agora m=n−1 e P(⋅) é o preço da put.
7 — Observações operacionais e conclusões
- A equivalência cardinal é uma equivalência da cauda (tail equivalence): garante que para S suficientemente alto (no caso calls) a combinação comporta-se como a posição vendida equivalente. Não é necessariamente igualdade de payoff em todas as faixas.
- Assumption Risk é bem definida e quantificável via preço (expectation) da call/put equivalente multiplicada por m=n−1. Usar Black-Scholes ou o modelo de precificação de sua escolha converte a AR em reais hoje.
- Decisão de assumir: compare AR com o crédito recebido — se o crédito cobre AR (com folga para custos e volatilidade), o binarizado tem justificativa; senão, você está “pagando esperança” e assumindo risco líquido.
- Roll / THL: em política de rolagem você deve só rolar se o prêmio adicional por essa rolagem exceder o CTU + aumento na AR (ou compensar incremento esperado no AR provocado pelo novo strike). Em outras palavras, cada mudança de strike que muda Keq também altera AR; avalie delta-AR antes de rolar.
- Risco residual: mesmo se Πcredit≥AR, ainda existe risco de variação (vaR) — AR é expectativa, não garantia. Use stress tests (gaps, IV spikes).
8 — Fórmulas-resumo rápidas (copiar/colar)
- m=n−1.
- Keq=n−1nK2−K1.
- AssumptionRiskper ac¸a˜o=m×C(S0,Keq,T,r,σ) (call-side).
- AssumptionRiskpor contrato=100⋅m⋅C(…).
- NetExposureExpected = AR − PremiumReceived.
para um Booster bem-estruturado em Calls, a perna comprada (+) deve ter o strike mais baixo; para o Booster em Puts, a perna comprada (+) deve ter o strike mais alto quando os dois boosters são conjugados (dual).
Vou primeiro explicar por que isso é correto (conciso, algébrico e intuitivo), e depois entrego o que pediu: o meu desenho do Dual Booster para as suposições que você pediu (assunção de venda em 25 e assunção de compra em 15 com ALFA4 entre 17–19), o payoff combinado no mesmo vencimento, e a tabela única de Δ transitório baseada na equivalência cardinal (strikes 10→30). Também disponibilizei a tabela CSV e o gráfico PNG (links abaixo).
1) Por que — regra das pernas compradas (call/put) e por que tenho que concordar
- Uma call longa tem payoff crescente a partir do seu strike: ela “liga” (slope +1) quando o preço sobe acima do strike. Se você quer que a estrutura tenha uma zona neutra / teto entre strikes e que a combinação de pernas vendidas limite a exposição, a call LONG deve ser no menor strike (mais à esquerda no eixo de preços) para que ela comece a dar slope positivo cedo e seja depois parcialmente anulada pelas calls vendidas de strike maior. Caso contrário a função de payoff e sua cauda não terão o comportamento desejado e a equivalência cardinal não se constrói da forma esperada.
- Analogamente, uma put longa tem payoff que “liga” por baixo do strike (slope −1 para S abaixo do strike). Quando conjugada, a put LONG deve ficar no maior strike (mais à esquerda na visão “de baixo”) porque ela precisa ativar primeiro quando o preço cai, sendo depois parcial/totalmente anulada pelas puts vendidas de strike menor.
- Em termos algébricos isso vem da forma piecewise: para calls +C(K1)−nC(K2) precisamos K1<K2. Para puts +P(K1)−nP(K2) precisamos K1>K2. Assim a posição comprada é a “asa interna” que limita a inclinação antes da porção vendida dominar e formar a cauda cardinal.
- Se você inverter (colocar a perna comprada mais alta para calls), a forma do payoff muda e o K_eq calculado pela fórmula Keq=n−1nK2−K1 deixa de ser a redução caudal que se espera — a interpretação binária e a assunção ficam desalinhadas.
Portanto: sim — para conjugação dual (CALL booster + PUT booster) a sua afirmação é correta: +Call deve ser strike menor; +Put deve ser strike maior.
2) Meu Dual Booster projetado (situação solicitada)
Condições: ativo ALFA4 entre R$17–R$19 (vamos tomar S0≈R$18 para referência), você quer:
- Assumption (venda) em 25 — isto é, equivalente cardinal de CALL-side será venda em K_eq=25.
- Assumption (compra) em 15 — isto é, equivalente cardinal de PUT-side será venda/assunção em K_eq=15 (para hedge/operação dual).
Escolhas (rácio n=2 — o caso clássico 2:1 → m = n-1 =1):
- Call booster: +C(Kc1)−2C(Kc2) com Kc1<Kc2.
- Escolhi Kc1=22.0 (call comprada) e Kc2=23.5 (duas calls vendidas).
- Equivalência cardinal: Kc,eq=2⋅23.5−22=25.0. → assunção de venda em 25.
- Put booster (DUAL): +P(Kp1)−2P(Kp2) com Kp1>Kp2.
- Escolhi Kp1=18.0 (put comprada) e Kp2=16.5 (duas puts vendidas).
- Equivalência cardinal: Kp,eq=2⋅16.5−18=15.0. → assunção de compra/entrada em 15.
Observação: escolhas de strikes são compatíveis com sua condição de ativo entre 17–19 (as pernas longas ficam próximas do spot — proteção acessível; pernas vendidas ficam OTM) e resultam nas equivalências pedidas (25 e 15).
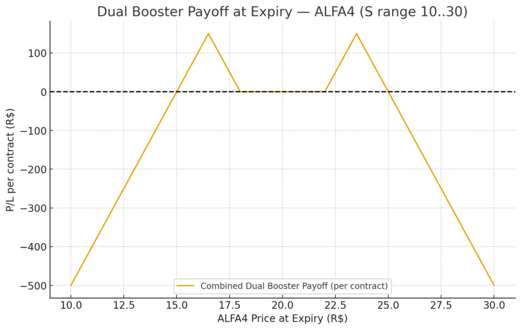
3) Payoff combinado no mesmo vencimento (gráfico & tabela)
- Eu calculei o payoff ao vencimento do conjunto (call booster + put booster) para S ∈ [10, 30] e gerei:
( já o exibi durante a execução — ele representa a forma “montanha dupla” com a zona neutra no centro.)
Resumo numérico rápido do payoff combinado:
- A zona entre aproximadamente 16.5–23.5 (dependendo do detalhe) costuma produzir payoff positivo (você recebe prêmio);
- Fora dessa zona (acima de 25 ou abaixo de 15) a exposição vira negativa (perdas lineares limitadas pela perna comprada remota), formando triângulos simétricos na cauda.
4) Tabela Única: Delta transitório baseada na equivalência cardinal (strikes 10→30)
Você pediu apenas 1 coluna com o delta transitório baseado na cardinalidade equivalente (isto é, a delta da posição equivalente binária construída pelos K_eq we chose: venda de Call em 25 e venda de Put em 15).
Usei a regra simples de delta ao vencimento para essas posições equivalentes:
- Delta de venda de Put K=15 (short put) ao vencimento: +1 quando S < 15 (pois long put delta = −1 there; short is +1); 0 quando S ≥ 15.
- Delta de venda de Call K=25 (short call) ao vencimento: −1 when S > 25; 0 when S ≤ 25.
- A delta combinada cardinal é, portanto:
- +1 se S < 15,
- 0 se 15 ≤ S ≤ 25,
- −1 if S > 25.
| S (R$) | delta_cardinal_equiv |
|---|---|
| 10.0 | +1.0 |
| 10.5 | +1.0 |
| ... | ... |
| 14.5 | +1.0 |
| 15.0 | 0.0 |
| 15.5 | 0.0 |
| ... | ... |
| 24.5 | 0.0 |
| 25.0 | 0.0 |
| 25.5 | -1.0 |
| 26.0 | -1.0 |
| ... | ... |
| 30.0 | -1.0 |
5) Explicação por que o delta cardinal tem essa forma (intuitiva e ligada à binarização)
- A equivalência cardinal transforma ambas as estruturas em dois contratos binários (curto call em 25 e curto put em 15). Esses dois contratos binários ativam apenas fora do intervalo [15,25].
- Dentro do intervalo [15,25] nenhum dos equivalentes está “ligado” — delta = 0; fora deste intervalo há um único lado ativo:
- abaixo de 15: short put atua (delta +1), pois a put comprada/vendida causa exposição positiva ao preço (vendedor de put tem delta +1 enquanto S muito baixo).
- acima de 25: short call atua (delta −1), vendedor de call tem delta −1.
- Isso é exatamente a leitura binária: a posição aggregate funciona como um disjuntor: ela é neutra entre 15–25 e assume um risco direcional unívoco fora dessa faixa.
6) Observações finais, recomendações operacionais e riscos
- A cardinalidade equivalente é poderosa para decisões de assunção (assumption): se você aceita ser “vendedor” em 25 e em 15 (binariamente), você aceita a exposição de cauda resumida; caso contrário mantenha a estrutura completa e avalie a exposição intermediária.
- Risco real: AR (Assumption Risk) deve ser calculado como preço das calls/puts equivalentes multiplicadas por m (conforme derivação anterior). Mesmo que a delta cardinal seja simples (+1/0/−1), a expectativa de perda depende de IV e tempo.
- Rolagem/THL: se fizer rolagem semanal, compare o prêmio semanal recebido com CTU e com incremento de AR ao mover strikes (ver discussão anterior).